5.5  Regressão

Esta opção processa uma regressão linear múltipla utilizando o método dos mínimos quadrados ordinários. São mostrados os coeficientes e estatísticas da regressão, podendo-se gerar gráficos da série ajustada contra observada e dos resíduos. É possível também gerar na área de trabalho a série ajustada e a série do resíduo e realizar testes de especificação e diagnósticos.

5.5.1 Estimando uma regressão

A partir da opção Econometria do menu principal, selecione Regressão para obter uma janela que solicita a especificação das variáveis e parâmetros. O mesmo efeito é obtido clicando-se no ícone  da barra de ferramentas.

Para estimar uma regressão linear o primeiro passo é selecionar a Variável dependente e as Variáveis independentes.

O número de variáveis independentes não pode ser superior a cinqüenta (50), sem considerar a Constante.

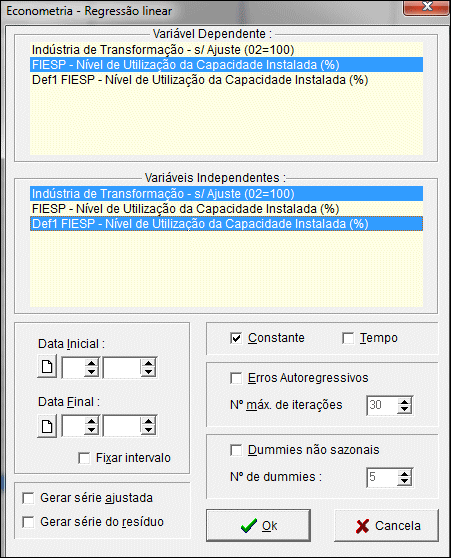
Especifique opcionalmente o intervalo a ser considerado na regressão nos campos Data Inicial e Data Final.

Caso não seja especificado o intervalo, o programa irá considerar o intervalo que vai desde a mais antiga até a mais recente observação disponível para as séries selecionadas.

Dica:

Marque a opção Fixar intervalo para manter o intervalo da última regressão processada nas próximas regressões.

As opções Gerar Série Ajustada e Gerar Série do Resíduo quando selecionadas criam na área de trabalho a série ajustada e a série de resíduo respectivamente, a partir dos coeficientes calculados pela regressão.

A opção Erros AR quando selecionada produz uma regressão com erros auto-regressivos. Neste caso são solicitados os termos auto-regressivos.

O campo Número de iterações é válido apenas para a regressão com erros auto-regressivos. Ele indica o número máximo de iterações do algoritmo até que haja convergência.

Após ter especificado os parâmetros, clique em Processar para obter a janela de saída, como mostrado na figura abaixo :

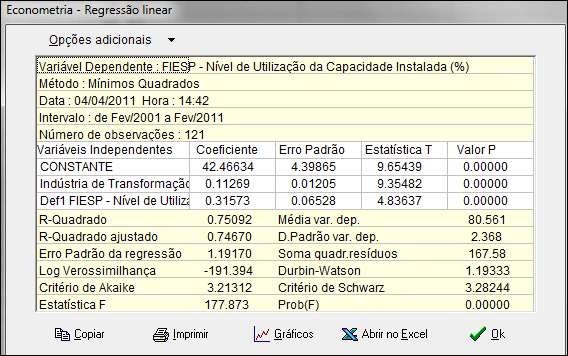
Para retornar à janela inicial de especificação da regressão, clique em Ok.

Dica:

Para rodar uma nova regressão com outras séries e intervalo diferente do intervalo da regressão anterior, clique nos botões de setas ao lado das datas para apagar as datas e considerar a data inicial mais antiga  e/ou a data final mais recente  .

5.5.2  Opções adicionais

A saída da regressão pode ser transferida para outros ambientes ou impressa : clique em Copiar para transferir para outro programa.

Clique em Editar-Colar no outro programa) ou em Imprimir para imprimi-la.

O botão Gráficos gera dois gráficos superpostos que servem para avaliar visualmente a qualidade do ajustamento e o comportamento dos resíduos.

Assim a qualidade da aderência da série ajustada sobre a série original pode ser avaliada graficamente, assim como a evolução temporal dos resíduos, que por hipótese deve seguir uma distribuição de probabilidade normal com média zero e variância um.

O primeiro gráfico apresenta os resíduos da regressão:

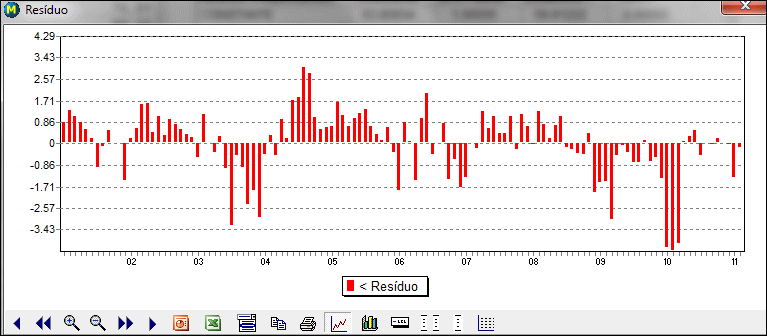
O segundo apresenta a série observada e a série ajustada:

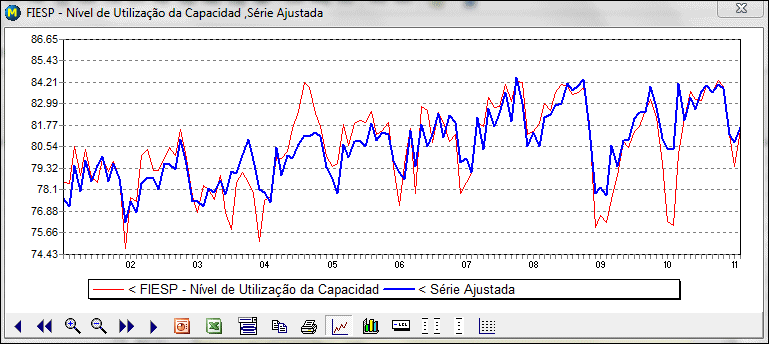
Note-se que esses gráficos podem ser livremente modificados, copiados ou impressos. Para mais informações sobre os recursos gráficos disponíveis, consulte o tópico Gráficos.

O botão Opções adicionais, que aparece na parte superior, aciona um menu de opções. A partir deste menu é possível obter outras janelas de saída úteis para avaliar a qualidade da especificação escolhida.

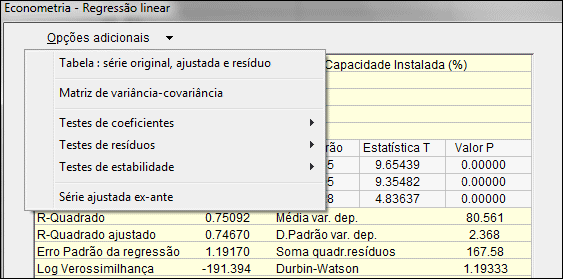
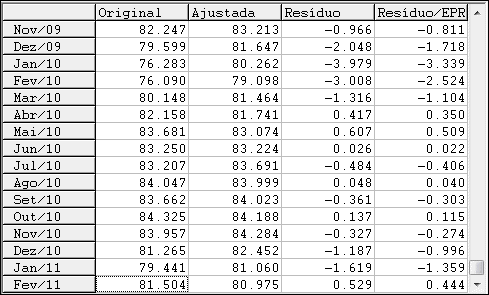
A primeira opção, Tabela : série original, ajustada e resíduo, leva a uma tabela com os valores originais e ajustados da variável dependente e os resíduos da regressão. 

A tabela inclui também os valores dos resíduos divididos pelo erro padrão da regressão (EPR) , o que corresponde à raiz quadrada da variância estimada dos resíduos.

Essa medida, indicada como “Resíduo/EPR”, é útil para identificar outliers entre os resíduos (p.ex. usando como critério valores maiores que 2). 

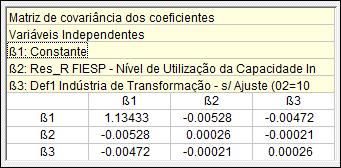
Também é possível obter a matriz de covariância dos coeficientes. A tabela de saída com a matriz de covariância pode ser impressa, copiada para outros ambientes ou aberta diretamente no Excel.

5.5.3 Interpretando a regressão

O modelo básico de regressão linear múltipla com N observações, uma constante e (k-1) variáveis independentes é:

Y(t) = b₀ + b₁* X₁(t) + ... + b _n* X_k-1(t) +  e (t)

, onde:

t é o marcador de tempo, variando de 1 até N,

Y(t) é o valor da variável dependente no período t,

b₀  é o termo constante,

X _j (t) é o valor da j-ésima variável independente no período t , com j variando de 1 a (k-1),

b_j  é o j-ésimo coeficiente associado à k-ésima variável independente,

e (t) é resíduo ou distúrbio aleatório no período t.

Em termos de notação matricial, isto equivale a:

Y = X b  + e

, onde Y é um vetor de dimensão N contendo as observações da variável dependente, b é um vetor de dimensão k contendo a constante e os coeficientes das (k-1) variáveis independentes,  X é uma matriz de dimensão (N x k) contendo todas as observações das variáveis independentes (inclusive uma coluna só com valores iguais a um para a constante)  e e é um vetor de dimensão N contendo os distúrbios aleatórios.

O método dos mínimos quadrados ordinários produz o vetor b como estimativa para o vetor teórico dos coeficientes b pela fórmula:

b = (X’X) ^-1 (X’Y)

Além dos coeficientes são também mostradas na janela de saída diversas estatísticas úteis para a análise do modelo adotado.

A coluna Erro padrão apresenta estimativas para os desvios padrão dsa distribuições dos coeficientes e seus valores permitem medir a confiança estatística que se pode ter com relação a essas estimativas:

Ø Quanto maiores forem os erros padrão, menor a confiança que se pode ter nos valores estimados. Se os resíduos forem normalmente distribuídos, existe aproximadamente 95% de probabilidade que cada coeficiente estimado esteja no intervalo entre dois erros padrão.

Os erros padrão podem ser obtidos tomando-se a raiz quadrada dos termos da diagonal da matriz de covariância dos coeficientes, definida por:

Var(b) = s² (X’X)^-1

,sendo s² a soma dos quadrados dos resíduos dividida pelos graus de liberdade da regressão (isto é, número de observações menos o número de coeficientes estimados):

s²  = e’e/ (N-k)

Note-se que  e  é o vetor de resíduos observados (que são as realizações observadas do resíduos teóricos e):

e = Y - Xb

A coluna Estatística T apresenta os resultados das divisões de cada coeficiente por seu respectivo erro padrão.

Sabe-se que quando os distúrbios aleatórios da regressão seguem uma distribuição normal, essas estatísticas seguem uma distribuição t de Student.

Com base nos valores conhecidos dessa distribuição é possível realizar testes de hipótese sobre os valores de determinado coeficiente.

Hipótese nula : o valor teórico do coeficiente é igual a zero

A coluna Valor P está associada ao nível de significância da estimativa (que é igual a um menos este valor). Quanto menor for seu valor, maior o nível de significância da estimativa e maior a confiança que se pode ter de que o coeficiente teórico não é igual a zero.

ü Se o valor-P for menor do que 0,05 a hipótese nula pode ser rejeitada com um grau de certeza de 95%, se a distribuição dos resíduos for normal.

A tela de saída da regressão também apresenta outras estatísticas úteis:

R-Quadrado é uma medida do grau do grau de proximidade entre os valores estimados e observados da variável dependente dentro da amostra utilizada para estimar a regressão, sendo portanto uma medida do sucesso da estimativa.

Pode ser interpretado (mas só quando a regressão inclui uma constante) como o percentual da variância da variável dependente que é explicada pelas variáveis independentes. O R-quadrado é calculado como :

R² = 1 – [e’e / ( y_m’ y_m) ]

, onde y_m é o vetor de observações da variável dependente transformadas para desvios em relação à média, isto é, o termo correspondente ao período t deste vetor é definido com

j=N 

y_m (t) = y(t) - (1/N) * S    y(j)

j=1  

ü R2 é próximo de 1 se o ajuste da regressão é perfeito ou próximo de zero caso contrário.

R-Quadrado ajustado é uma medida semelhante ao R-quadrado mas que, ao contrário deste, não aumenta com a inclusão de variáveis independentes não significativas.

Dessa forma evita-se o problema característico do R-quadrado, que tende a  aumentar sempre que são adicionadas novas variáveis independentes, mesmo que contribuam pouco para o poder explicativo da regressão. O R-quadrado ajustado é calculado como :

_

R² = 1 – [ (1- R²)*(N-1) / (N-k) ]

Soma dos quadrados dos resíduos é uma medida útil para vários cálculos estatísticos, sendo definido como:

SQR  = e’e

Erro padrão da regressão é a raiz quadrada da variância estimada dos resíduos e indica o grau de dispersão dos erros de previsão dentro da amostra na hipótese de normalidade. O erro padrão da regressão é calculado como:

s  = Raiz quadrada( SQR / (N-k))

Média e Desvio Padrão da variável dependente são medidas relativas à posição e formato da distribuição da variável dependente que se está tentando explicar na análise de regressão.

O erro padrão da variável dependente pode ser calculado a partir do vetor de observações da variável dependente transformadas para desvios em relação à média (y_m), como:

s_y  = Raiz quadrada(( y_m’ y_m) / (N-1))

Durbin-Watson é uma medida do grau de correlação serial de ordem um (ou AR(1)) dos resíduos. Pode ser calculado como:

t=N 

DW  =  S  ( e_t – e _t-1 )² / (SQR)

t=2

Ø Como regra de bolso, admite-se um DW menor do que 1,5 como evidência de correlação serial positiva e um DW maior do que 2,5 como evidência de correlação serial negativa.

Pode-se derivar do DW uma estimativa para o coeficiente de correlação serial dos resíduos, pois:

r= 1 – 0,5*DW   aproximadamente,  se  e_t  = r*e _t-1

Log Verossimilhança é o valor do logaritmo da função de verossimilhança (na hipótese de erros com distribuição normal) calculado para os valores estimados dos coeficientes.

Esta estatística serve para testes de razão de verossimilhança, que avaliam a diferença entre seus valores para versões com restrição e sem restrição da equação de regressão.        

A estatística log verossimilhança (L) é calculada por:

L = - (N/2)*(1+ log (2p) + log (SQR/N)

,sendo SQR a soma dos quadrados dos resíduos e N o número de observações.

Critério de Informação de Akaike é uma estatística freqüentemente utilizada para a escolha da especificação ótima de uma equação de regressão no caso de alternativas não aninhadas.

Dois modelos são ditos não aninhados quando não existem variáveis independentes comuns aos dois.

ü Quando se quer decidir entre dois modelos não aninhados, o melhor é o que produz o menor valor do critério de Akaike

Por exemplo, o número de defasagens a serem incluídas numa equação com defasagens distribuídas pode ser indicado pela seleção que produz o menor valor do critério de Akaike.

O critério de Akaike (AIC)  é definido como:

AIC =  2 * (k-L) / N

, onde L é a estatística log verossimilhança, N o número de observações e k o número de coeficientes estimados (incluindo a constante).

Critério de Schwarz é uma estatística semelhante ao critério de Akaike com a característica de impor uma penalidade maior pela inclusão de coeficientes adicionais a serem estimados. O critério de Schwarz (SIC) é definido como:

SIC =  (k*log(N) – 2*L) / N

Estatística F é a estatística utilizada para testar a hipótese de que todos os coeficientes da regressão (excluindo a constante) são nulos. Pode ser calculada como:

F = [ R² / (k-1)] / [ (1- R²) / (N-k) ]

Na hipótese de que os resíduos teóricos têm distribuição normal, essa estatística tem uma distribuição F com (k-1) graus de liberdade no numerador e (N-k) graus de liberdade no denominador.

Hipótese nula : o valor teórico de todos os coeficientes

 (excluindo a constante) é igual a zero

Para testar a hipótese nula usaremos a Prob(F), descrita a seguir.

Prob(F) é o nível de significância associado à estatística F calculada.

ü Se Prob(F) for menor do que um determinado nível de significância, digamos 5%,  a conclusão é que podemos rejeitar a hipótese nula.

Note-se que como a estatística F é usada para testar uma hipótese conjunta, ela pode ser altamente significante mesmo quando todas as estatísticas-t individuais forem insignificantes.